シンプルチェーン

シンプルチェーン(Simple Chain)とは、 「ある候補が３つの強リンクでチェーン」 になったもので、 「チェーンの両端の交点には、その候補を配置できない」 です。

そのため、シンプルチェーンは 「未確定が7つ以上(確定している候補は4つ程度)残っている状態」 で使うテクニックです。

強リンクとは、「ある候補が行(または列,Box)で2つだけに限定されている」ものです。チェーン系のテクニックで活用します。

シンプルチェーンはX-Chainとも呼ばれています。そしてシンプルチェーンはSingle's Chains(Simple Colors)と同等のテクニックです。

基本編

ここではシンプルチェーンの基本となるパターンを見て行きます。

候補1に注目して候補を洗い出してみます。

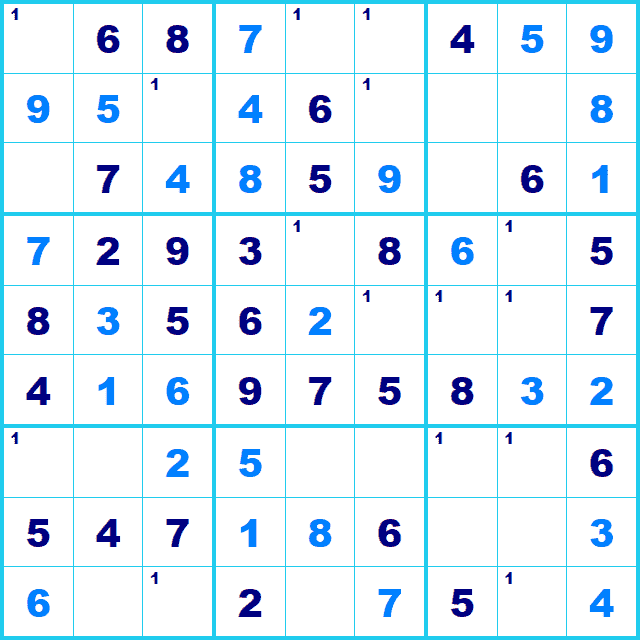
行または列かBoxで2つに限定された候補に注目します。

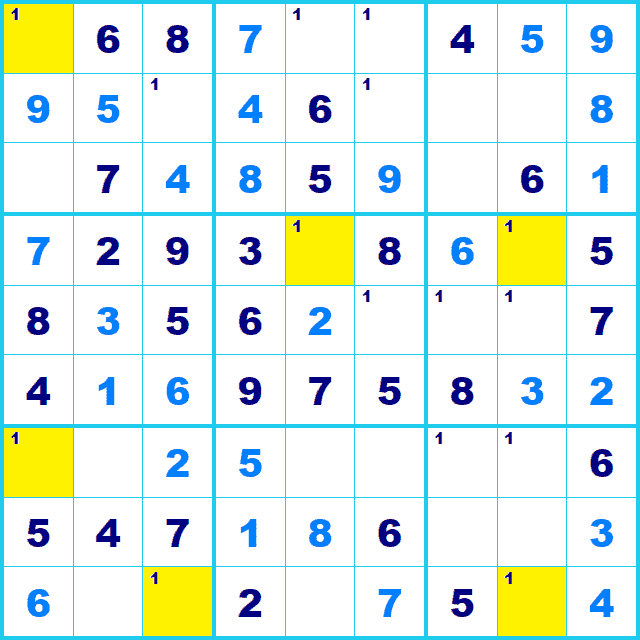
2つの候補をつないで確認してみます。これが強リンクです。

強リンクは時々目にする用語ですが、つまり「どちらか」ということですね。

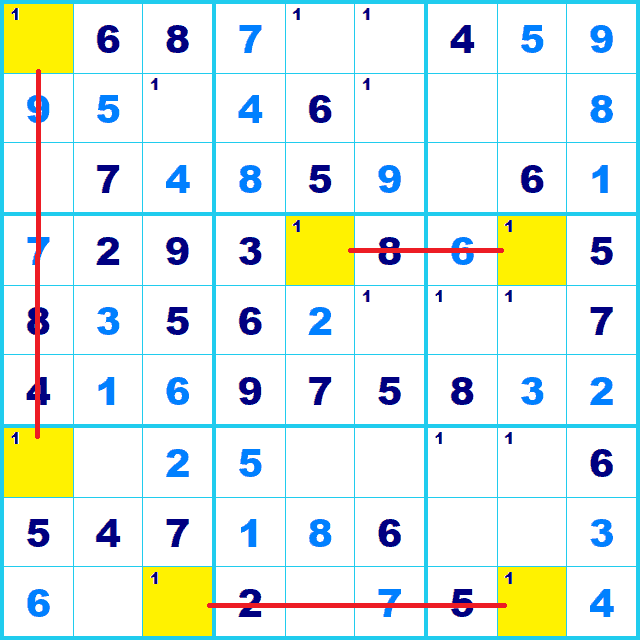
そして強リンクを3つ繋いでみます。この時、同一行または列かBoxであることです。

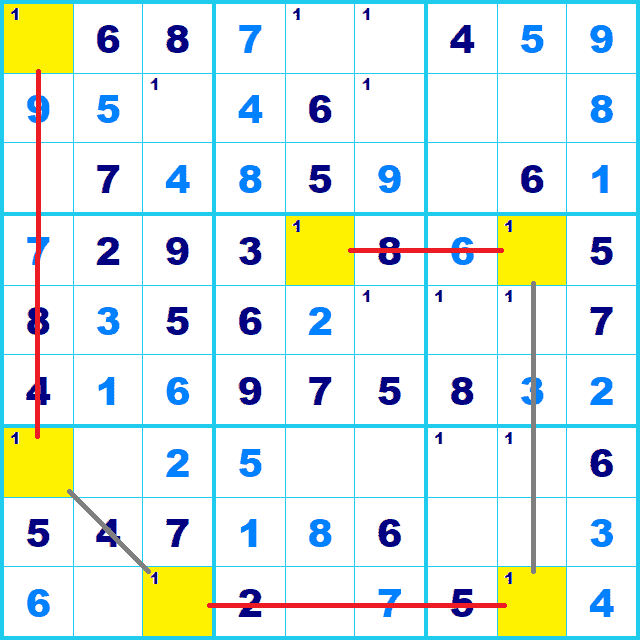
強リンクは「どちらか」です。リモートペアの解説と同様に、確定した場合を想定して交互に候補を置いてみると、シンプルチェーンの両端(オレンジのマス)の交点(灰色のマス)にはその候補(ここでは候補1)が配置できません。

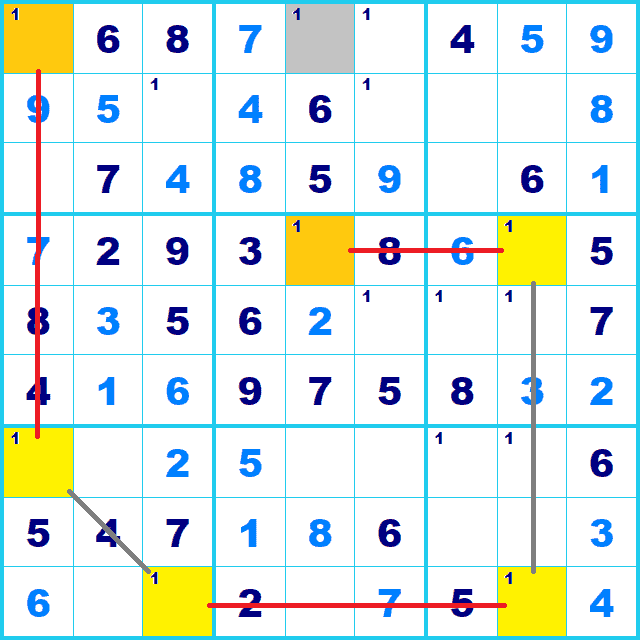
「偶数個で連なる一本のチェーン」がシンプルチェーンのキーポイントです。

シンプルチェーンの両端の交点の候補が消去できる場合です。

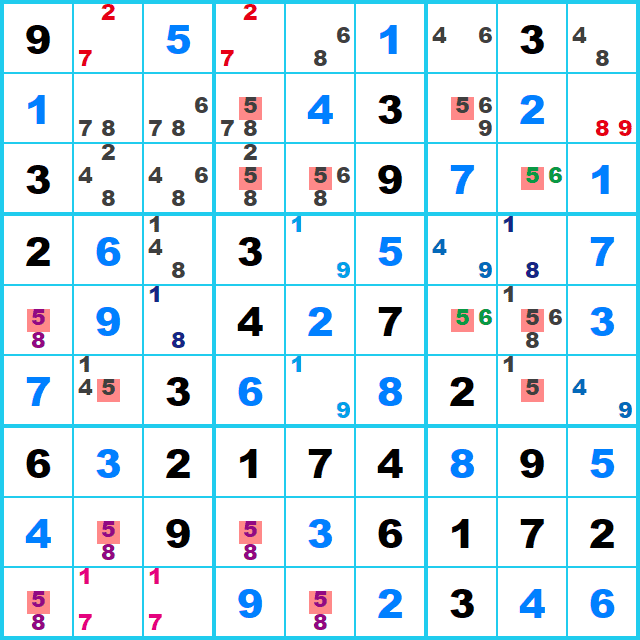
ここでは候補5に注目して候補を洗い出してみます。

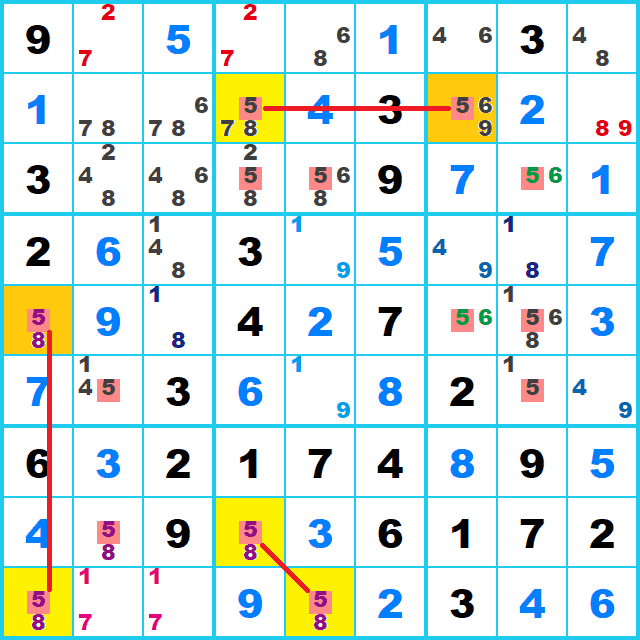
行または列かBoxで2つに限定された候補5を探してみると、行2,列1,下段中央のBoxに見つかります。

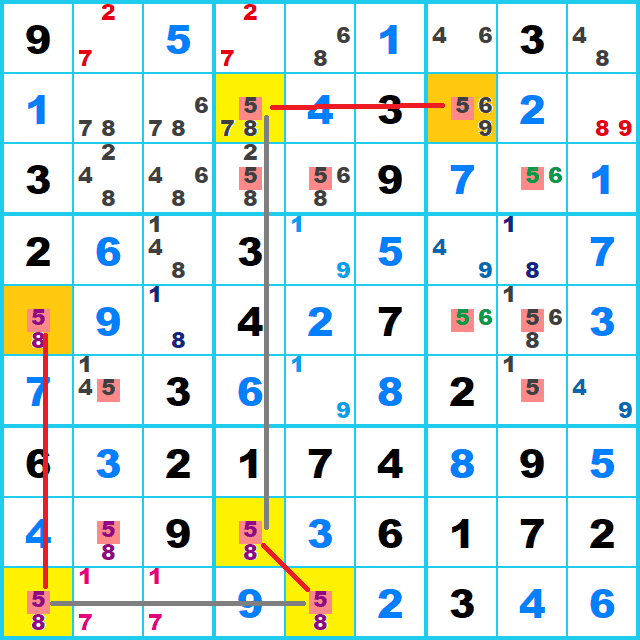
このようにそれそれが同じ行または列かBoxにあればつながります。ひとマスでも外れていれば成立しません。

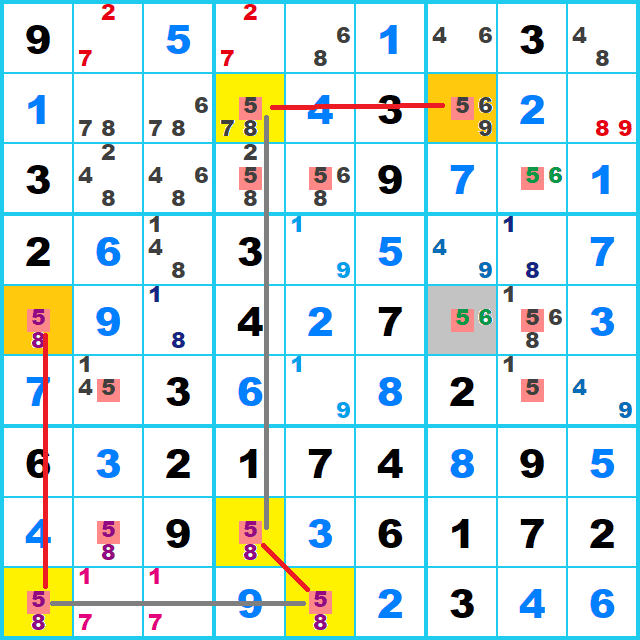
つながれば両端(行2列7,行5列1)(オレンジのマス)の交点(行5列7)(灰色のマス)にある候補5を消去できます。両端のBoxがタテでもヨコでも揃っていないので、両端の交点の候補を消去できるパターンです。

シンプルチェーンの両端のBox内の同じ行(または列)にある候補を消去できる場合です。

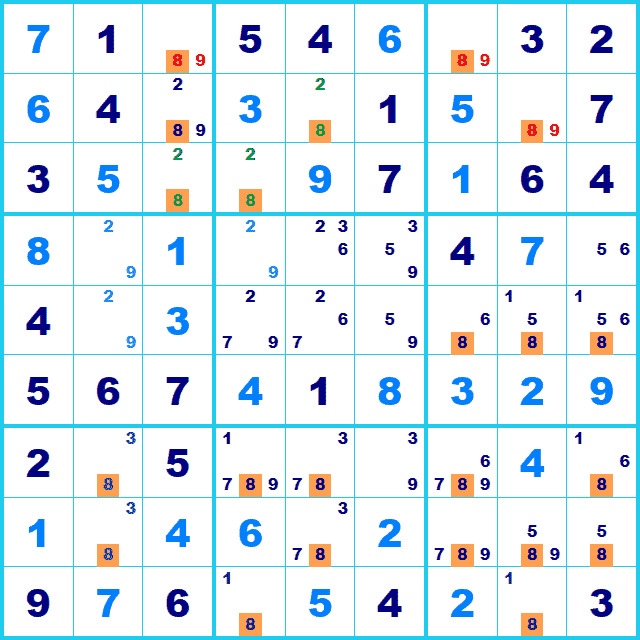
ここでは候補8に注目して候補を洗い出してみます。

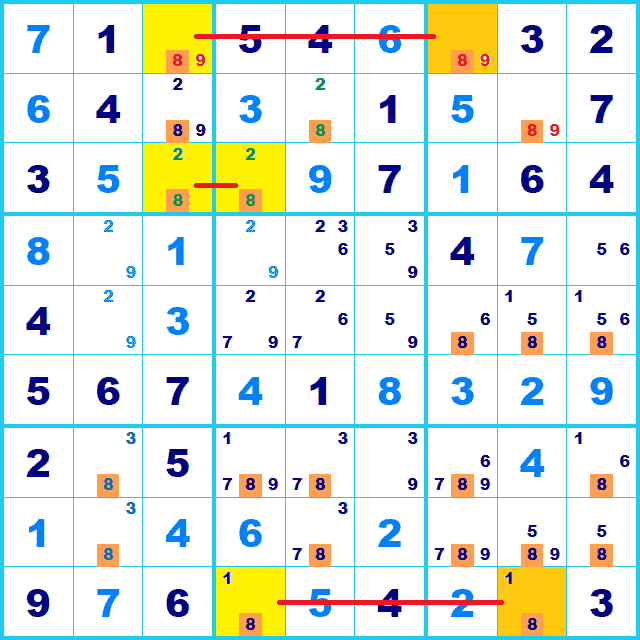
行または列かBoxで2つに限定された候補8を探してみると、行1,行3,行9に見つかります。

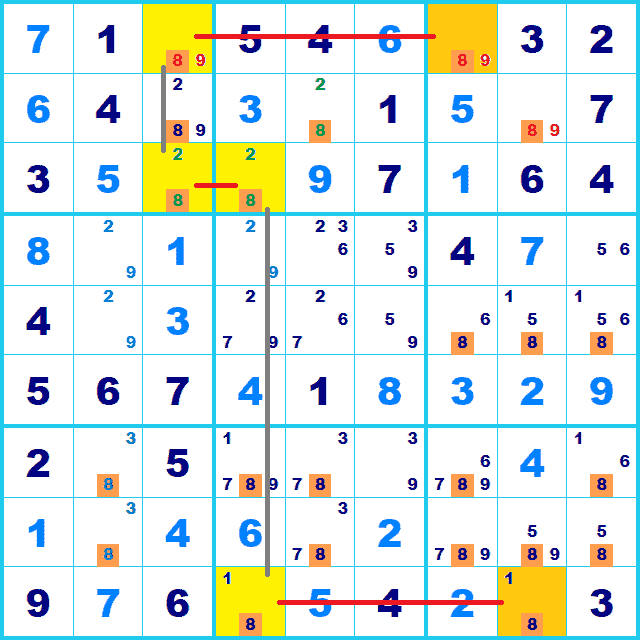
このようにそれそれが同じ行または列かBoxにあればつながります。ひとマスでも外れていれば成立しません。

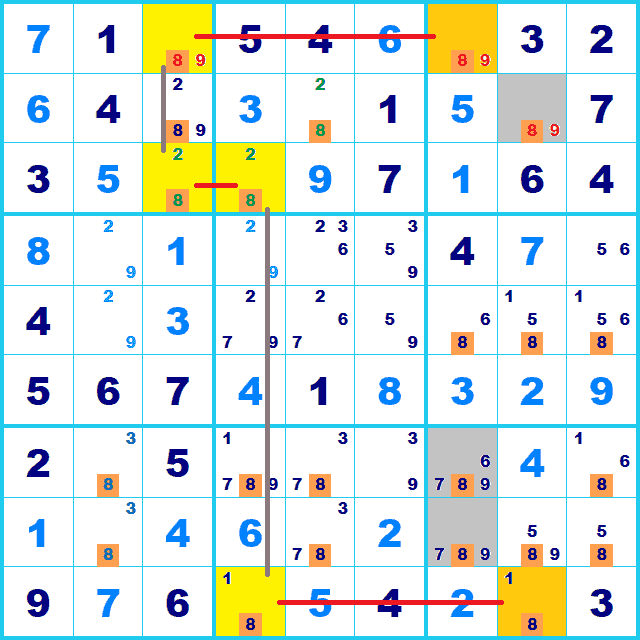
つながれば両端のBox内にある同じ列(行2列8,行7列7,行8列7)(灰色のマス)にある候補8を消去できます。両端のBoxがタテで揃っているので、両端の延長線上にあるBox内の候補を消去できるパターンです。