WXYZウィング

WXYZウィング(WXYZ-wing)とは、XYZウィングを発展させたもので、 「4つの候補が4つのマスを使って三角形のように配置される」 です。この時Boxを2(or3)つ使います。

四国同盟は「4マスとも同じ行(また列,Box)にあります」が、WXYZウィングは「4つ目のマスは4つの候補を使うマスと同じBoxにある」ことになり、直線上(同じ行または列)にはありません。

候補はwxyzのように4コ入るマスが1つ、wz,xz,yzのように2コ入るマスが3つあります。

3マスは同じ行(または列)で別Boxにあり、残りの1マスは4コ入るマスと同じBoxに存在します。

wzのマスが同じ行(または列)にはないので、四国同盟に成り損ねたとも見て取れます。

基本編

ここではWXYZウィングの基本となるパターンを見て探し方を考えていきます。

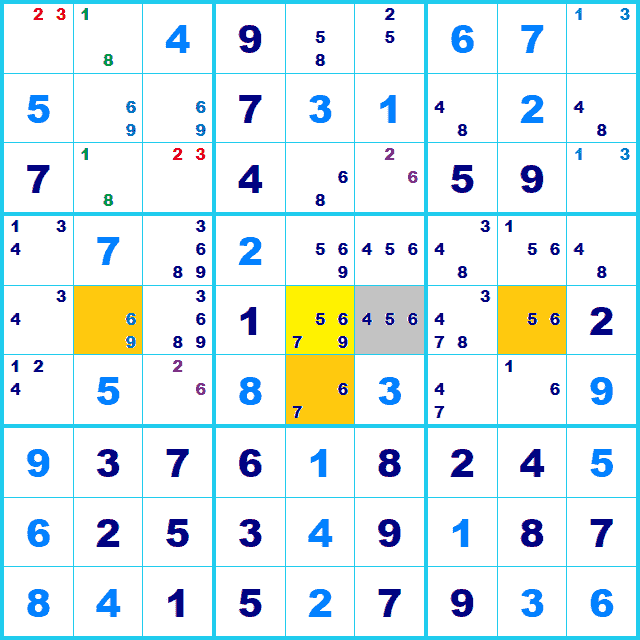
候補9は行1列2,行3列1,行3列5,行3列8(オレンジか黄色のマス)のどこかに入ります。この場合どこに入っても行3列2、行3列3の2マス(灰色のマス)に候補9は置けません。

WXYZウィングを探す過程は、同一行(または列)に候補数4のマスと候補数2のマスを2つ見つけます。候補数4のマスには候補数2のマスの候補が含まれています。

4つ目のマスは候補数4のマスのBoxから探し出します。この時候補になるのは3つに共通した候補9と単独の候補1です。

そして4つのマスに共通する候補9は灰色のマスに入りません。

行(または列)が一致するとNGパターンです。これは 4国同盟です。

今日の難問ナンプレを見る

ここでは行5の候補5,6,7,9に注目して候補を洗い出してみます。

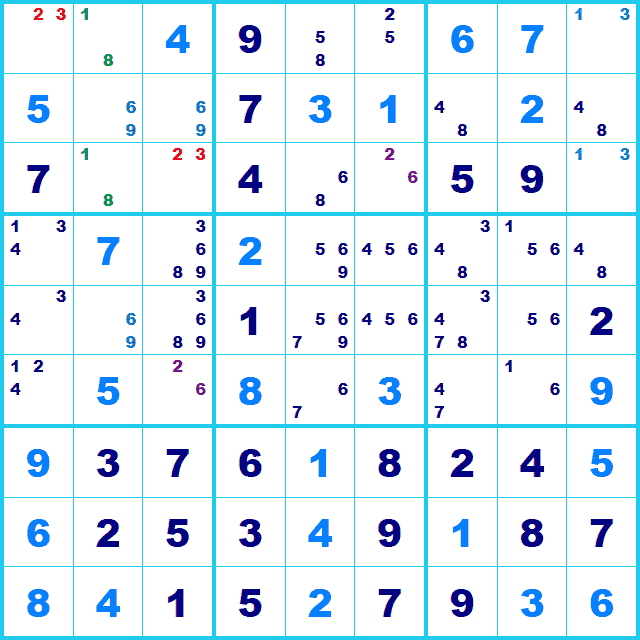
行5列2の候補6,9と行5列5の候補5,6,7,9と行5列8の候補5,6があります。 3マスで候補を4つ使っています。

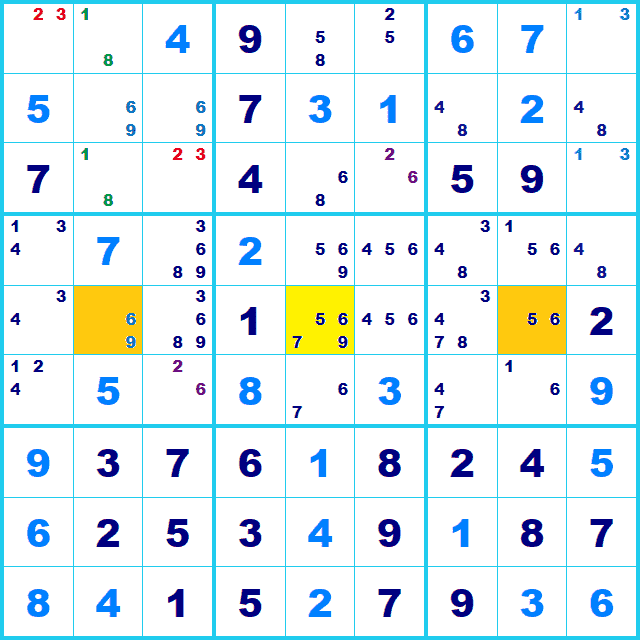
4つ目のマスを候補数4のマス(黄色)があるの中段中央のBoxから探し出します。ここでは「候補6,7」があるマスが行6列5にあります。

候補6はこの4つのマスのどこに入ったとしても行5列6(灰色のマス)には置けません。それによって、行5列6にある候補6を消去できます。

今日の難問ナンプレを見る