BUG

BUGとは、「候補数3のマスが1つで、残りのマスが全て候補数2の場合、候補数3のマスの候補の中で行(または列,Box)で3カ所で候補になっている数字は確定できる」です。

基本編

BUGは、 「ナンプレの答えは1つのみ」 を前提としたテクニックです。

仮に、最後の4マスが候補1,２のどちらかの場合、答えが２つあり、残念な問題です。 (この問題は最後の4マスに候補1,２が入る前提で特別に作成しています。)

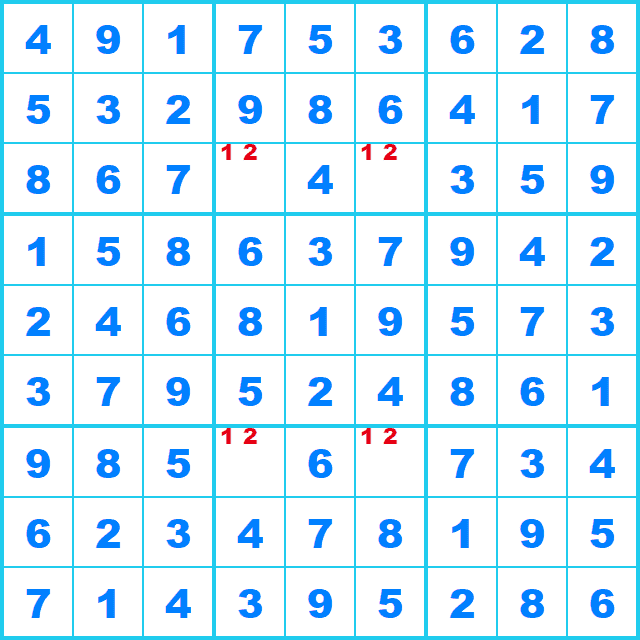
そして、BUGは、この 「残りのマスは候補2つと候補3つ」 の関係を利用するので、 「見つけた時点で詰み」 といえるテクニックです。

「候補3つのマスが1つで、残りのマスが全て候補2つ」 であること。 (残り全てが候補2つのマスにならないことが前提です)

では残り13マスで、「候補3つのマスが1つ(黄色のマス)で、残りのマスが全て候補2つ」が成立した局面です。

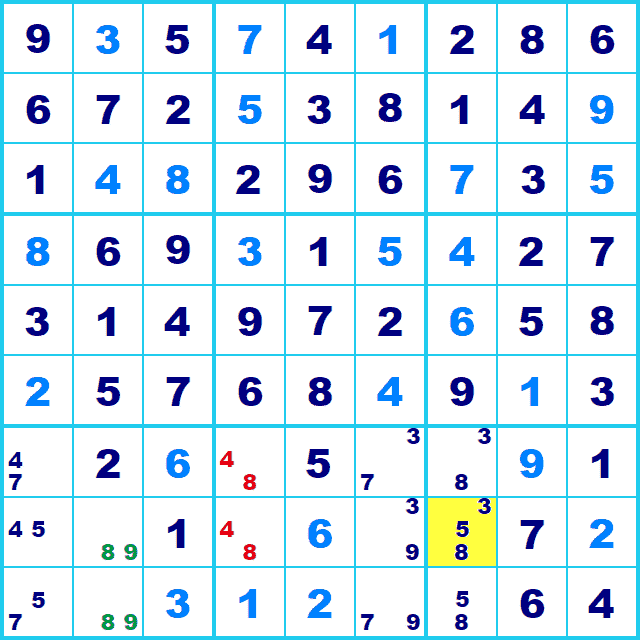
仮に候補が3つのマスに、3を入れた場合は矛盾します。

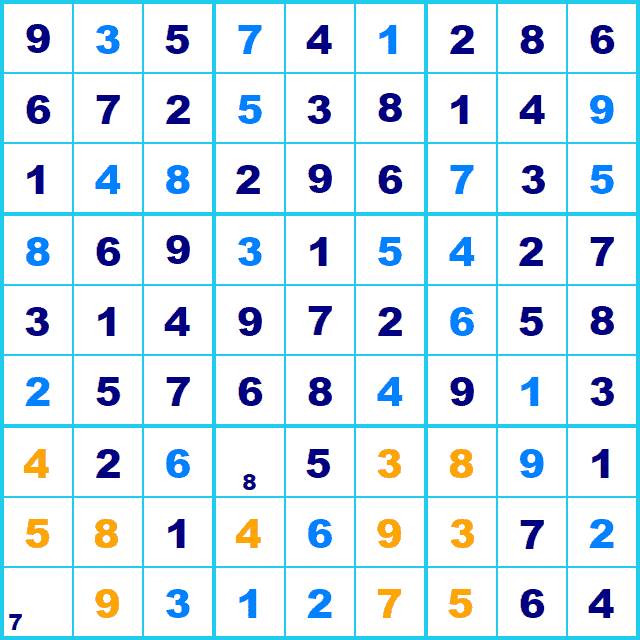
そして仮に、5を入れた場合も矛盾します。

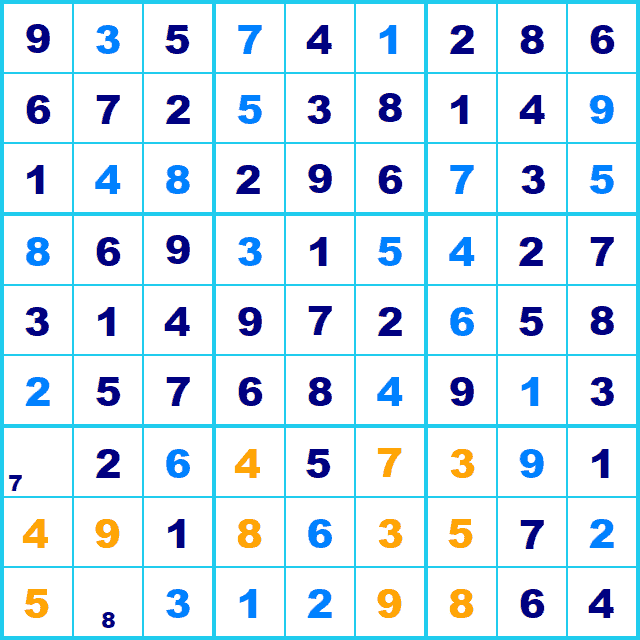
つまり、行(または列,Box)で3カ所で候補になっているものを確定します。とてもシンプルです。ここでは候補8ですね。

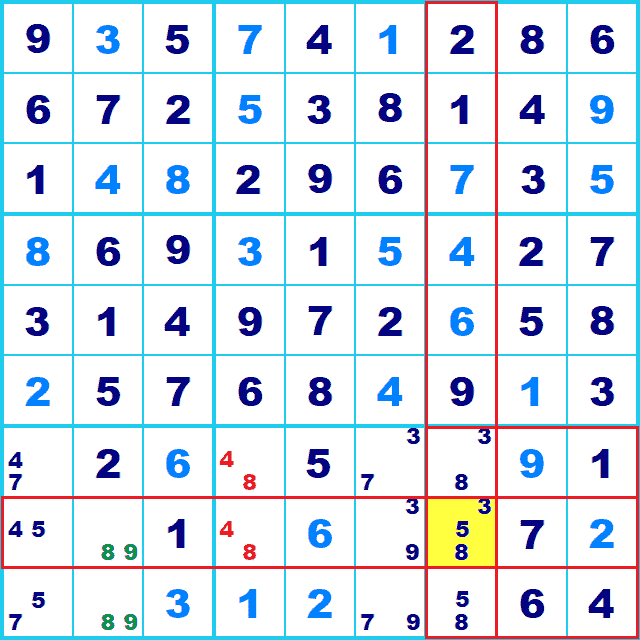
BUGのテクニックを使えば、この残り13マスの場面を悩む必要もなくゴールまで導きます。

これらのことから、XY-Chainを使う前に当てはまるか確認しておきたいシンプルで強力なメソッドです。

残り21マスで、XY-Chainを試みる局面ですが、BUGを覚えていれば意外にもあっさりと解けます。

ここでは候補が3つのマスに注目してみます。

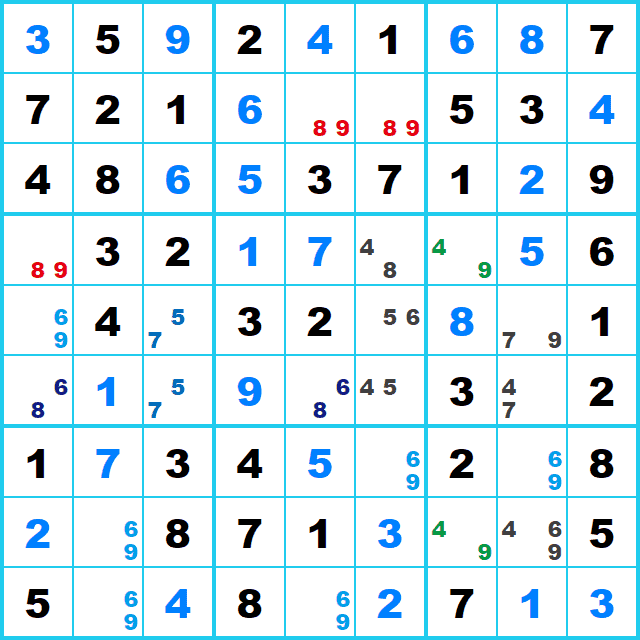
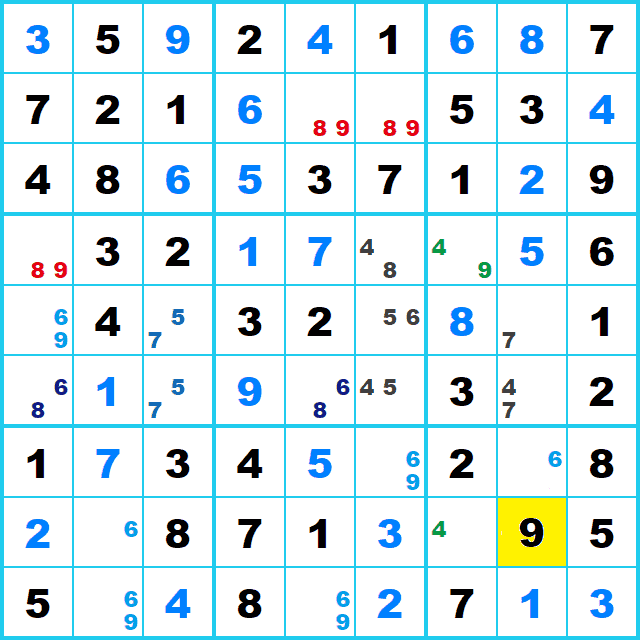
行8列8(黄色のマス)は候補が3つです。それ以外のマスの候補は2つです。

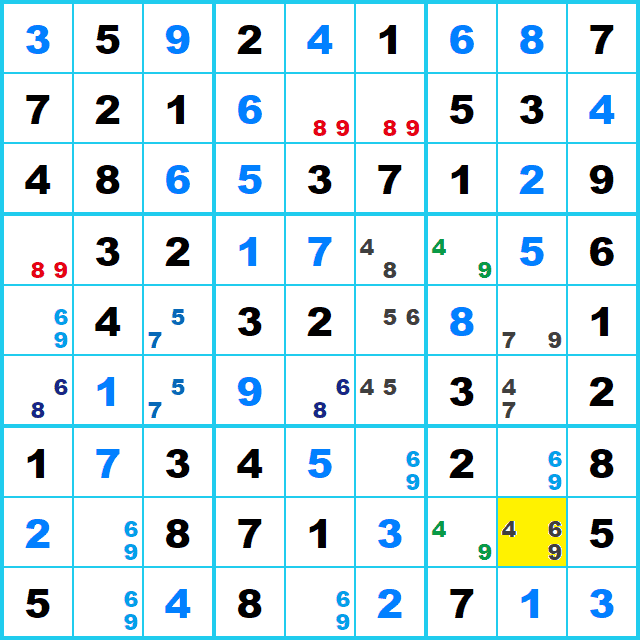
この時、行8では候補9が3回候補に上がっています。

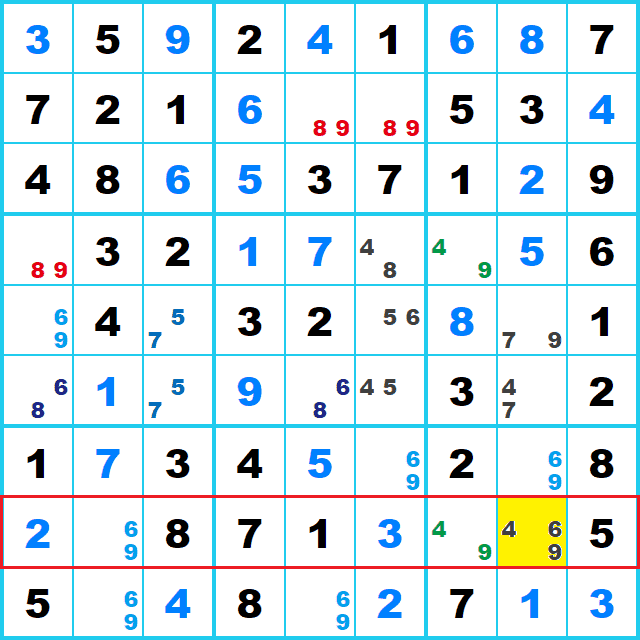
候補9が確定になり、ここから先はシングル(Singles)だけで最後まで行けます。

これを覚えているだけで上級問題が簡単に感じる場面が出てきます。